Triangulations
A triangulation of a set S of points is a partition
of the convex hull of S into
triangles. This assumes that not all points of S are collinear.
Strengths
On the right you see a triangulation of a set of points in the plane, the points and edges on the convex hull are drawn in red. The picture is a screenshot from the example of computing and verifying a triangulation. |
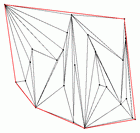 |
Example of computing and verifying a triangulation
Representation
The triangulation is represented by the parameterized graphGRAPH<POINT,int> G. G is a straight
line embedded plane map. It corresponds to the triangulation T
of the set of points L as follows:
- Nodes are in one-to-one correspondence with the points in
L Gis bidirected- For each node
vofGthe listA(v)of edges out ofvis ordered cyclically. This cyclic ordering agrees with the counter-clockwise ordering of the edges incident to the point inTcorresponding tov. - Each edge
eofGhas an integer label that gives information about the edge.G[e]=2ifeis on the convex hull ofLG[e]=0ifeis on the Delaunay Diagram ofLG[e]=1otherwise
Running Time
The algorithm is an extension of the sweep algorithm for convex hull. The running time isO(nlogn).
Verifying Triangulations
The functionbool Is_Triangulation(GRAPH<POINT,int>& G)
returns true if G is a convex planar subdivision in which
every bounded face is a triangle or all nodes of G lie on
a common line. See also Verification of Geometric
Structures.
POINT to indicate that the algorithm works both for
points and rat_points. See also Writing
Kernel Independent Code.
Algorithms for Constrained Triangulations
LEDA provides additional algorithms for computing triangulations of segments, plane maps, and polygons. Details can be found on the Manual Page of Geometry Algorithms.See also:
Writing Kernel Independent Code
Verification of Geometric Structures