Delaunay Diagrams

A Delaunay diagram of a set S of points consists of the segments that belong to all (furthest site) Delaunay triangulations of S.

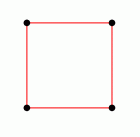
On the right you see a Delaunay diagram of a set of four points placed at the corners of a square. The two possible Delaunay triangulations for the points can be build from the diagram by adding one of the two diagonals of the square. The picture is a screenshot from the example of computing and verifying a Delaunay diagram.

Properties of Delaunay Diagrams

• A Delaunay diagram is a subgraph of every Delaunay triangulation.
• The Delaunay diagram is a planar graph whose bounded faces are convex polygons all of whose vertices are co-circular.
• If no four points of S are co-circular then all bounded faces are triangles and the Delaunay diagram is a triangulation.

Running Time

The running time of the algorithms is O(n²).

Verifying Delaunay Diagrams

	bool Is_Delaunay_Diagram(const GRAPH<POINT,int>& G, 
	                           delaunay_voronoi_kind kind)

checks whether G is a Delaunay diagram of the points associated with its nodes. The flag kind allows to choose between the nearest (kind=NEAREST) and furthest (kind=FURTHEST) site version. See also Verification of Geometric Structures.

We use the notation POINT to indicate that the algorithm works both for points and rat_points. See also Writing Kernel Independent Code.

See also:

Data Types for 2-D Geometry

Delaunay Triangulations

Voronoi Diagrams

Euclidean Minimum Spanning Trees

Convex Hulls

Triangulations

Verification of Geometric Structures

Writing Kernel Independent Code

Geometry Algorithms

Geometry

Graphs

GeoWin

Manual Entries

Manual Page of Geometry Algorithms