The Edit-and-Run Paradigm

The edit-and-run paradigm for interactive demos of graph algorithms looks as follows. We define a GraphWin gw and open it. Then we enter the edit-loop. In the edit-loop the graph G associated with gw is modified interactively or a new graph is generated using one of the graph generators. After the edit operations the graph algorithm is run on G by pressing the done-button of gw and the result is displayed. The following generic program illustrates the paradigm.

If you want to show the result of a graph algorithm while you are editing the graph (without clicking the done-button), have a look at A Recipe for Online Demos of Graph Algorithms. If your graph has edge capacities or costs have a look at A Recipe for Online Demos of Network Algorithms.

#include <LEDA/graphics/graphwin.h>
#include <LEDA/graph/graph_alg.h>

using namespace leda;

int main()
{
  GraphWin gw("Edit-and-Run Paradigm");
  gw.display(window::center,window::center);
		
  while (gw.edit()) {
    graph& G=gw.get_graph();
    //run graph algorithm on G and display result
  }
	
  return 0;
}

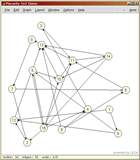
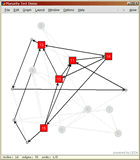
Planarity Testing with Edit-and-Run

We use the edit-and-run paradigm to test the graph G for planarity. If G is planar and has at least three nodes, we compute a straight line embedding and display the resulting layout (see also Graph Drawing Algorithms). If the graph is non-planar, we compute a Kuratowksi subdivision K=(V_k,E_k) and display it by calling a highlight()-function. We wait until the user clicks done and then restore the old drawing.

On the right you see screenshots of the program for a non-planar graph. The first picture shoows the original graph and the second picture the result of the highlight()-function. Clicking on the pictures shows the Graphwin in original size.

#include <LEDA/graphwin.h>
#include <LEDA/graph_alg.h>

using namespace leda;

//run graph algorithm and display result
void run_and_display(GraphWin& gw);		

int main()
{
  GraphWin gw("Planarity Test Demo");
  gw.display(window::center,window::center);
		
  while (gw.edit()) {	
    gw.get_window().screenshot("gw_planarity_original");
    run_and_display(gw);
  }
		
  return 0;
}
	
//plandemo highlight
void highlight(GraphWin& gw, const list<node>& V, 
               const list<edge>& E,node_array<int>& kind);

void run_and_display(GraphWin& gw)
{
  graph& G=gw.get_graph();
		
  if (PLANAR(G)) {
    if (G.number_of_nodes()<3) return;
			
    node_array<double> xcoord(G);
    node_array<double> ycoord(G);
    STRAIGHT_LINE_EMBEDDING(G,xcoord,ycoord);
    gw.adjust_coords_to_win(xcoord,ycoord); 
    gw.set_layout(xcoord,ycoord);
  }

  else {
    list<node> V_k;list<edge> E_k;
    node_array<int> kind(G);
    KURATOWSKI(G,V_k,E_k,kind);
			
    gw.save_all_attributes();
    highlight(gw,V_k,E_k,kind);
    gw.wait("This graph is not planar. I show you a \
             Kuratowski subdivision (click done).");
    gw.restore_all_attributes();
  }
}

void highlight(GraphWin& gw, const list<node>& V, 
       const list<edge>& E,node_array<int>& kind)
{
  const graph& G=gw.get_graph();
  bool flush0=gw.set_flush(false);
		
  node v;forall_nodes(v,G) {
    switch (kind[v]) {
    case 0: gw.set_color(v,grey1);
            gw.set_border_color(v,grey1);
            gw.set_label_color(v,grey2);
            break;
    case 2: gw.set_color(v,grey1);
            gw.set_label_type(v,no_label);
            gw.set_width(v,8);
            gw.set_height(v,8);
            break;
    case 3:
    case 4: gw.set_shape(v,rectangle_node);
            gw.set_color(v,red);
            break;
    case -3: gw.set_shape(v,rectangle_node);
             gw.set_color(v,blue2);
             break;
    }
  }
		
  edge e;
  forall_edges(e,G) gw.set_color(e,grey1);
  forall(e,E) {
    gw.set_color(e,black);
    gw.set_width(e,2);
  }
		
  gw.redraw();
  gw.set_flush(flush0);

  gw.get_window().screenshot("gw_planarity_highlight");
}