Orthogonal Algorithms
Graphs can be used to represent relational information. This is the reason why it is often useful to draw graphs in order to visualize this relational information.
Orthogonal Algorithms draw planar graphs in such a way that all edges are sequences of horizontal and vertical segments. The nodes and edge bends are placed on integer coordinates. Obviously, we need a strategy to deal with nodes that have more than four incident edges. One strategy is to allow that in a small region around such nodes the edges can be drawn arbitrarily. Another strategy is to draw high-degree nodes as rectangles covering more than one integer coordinate.
LEDA Functions for Orthogonal Drawings
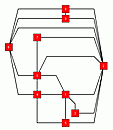
ORTHO_EMBEDDING(): Let G=(V,E) be a
planar graph. ORTHO_EMBEDDING() computes an orthogonal drawing
where the edges around high-dregree nodes are drawn arbitrarily in a (relatively)
small region.
Example ORTHOGONAL_EMBEDDING()
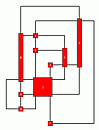
ORTHO_DRAW(): Let G=(V,E) be a planar
graph. ORTHO_DRAW() computes an orthogonal drawing where
the high-dregree nodes are made bigger in order to draw the incident edges
horizontally and vertically.
Tips
In practice, orthogonal drawings are among the best.
See also:
Manual Entries:
Manual Page Graph Drawing Algorithms