Guide > Geometry Algorithms > Extremal Circles

Extremal Circles

The functions discussed here are direct applications of Voronoi diagrams.

Smallest Enclosing Circle

The smallest enclosing circle for a set L of points is the circle with the smallest radius containing all points in L. Such a circle has at least two points in L on its boundary and its center lies on the furthest site Voronoi diagram of L.
The center is either a vertex of the furthest site Voronoi diagram (three vertices of L on its boundary) or lies on an edge (two sites on the boundary).

On the right you see a smallest enclosing circle of a set of 10 points in the plane. The picture is a screenshot from the program below.

 Picture of Smallest Enclosing Circle

Largest Empty Circle

The largest empty circle for a set L of points is the circle with the largest radius whose interior is void of points in L and whose center lies inside the convex hull of L. Such a circle has at least two points in L on its boundary and its center lies on the nearest site Voronoi diagram of L.
The center of the circle is either a vertex (three vertices of L on its boundary) or lies on an edge of the Voronoi diagram (two sites on the boundary).

On the right you see a largest circle of a set of 10 points in the plane. The picture is a screenshot from the program below.

 Picture of Largest Empty Circle

All Enclosing Circles

All Empty Circles
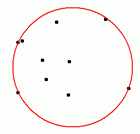
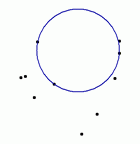
Picture of Largest Empty Circle
Picture of Largest Empty Circle
LEDA also provides functions to compute the list CL of all enclosing (picture on the left) and all empty (picture on the right) circles passing through three or more points of L.

Example Program for Computing Extremal Circles

The following program computes the extremal circles and was used to generate all pictures above.

#include <LEDA/core/list.h>
#include <LEDA/geo/rat_point.h>
#include <LEDA/geo/rat_circle.h>
#include <LEDA/geo/random_rat_point.h>
#include <LEDA/graphics/window.h>
#include <LEDA/geo/geo_alg.h>

using namespace leda;

int main()
{
  list<rat_point> L;
  random_points_in_square(10,50,L);  

  rat_circle C;
  //C=SMALLEST_ENCLOSING_CIRCLE(L);
  //C=LARGEST_EMPTY_CIRCLE(L);

  list<rat_circle> LC;
  ALL_ENCLOSING_CIRCLES(L,LC);
  //ALL_EMPTY_CIRCLES(L,LC);

  window W;
  W.init(-110,110,-110);
  W.open(); W.display();
  W.set_node_width(3); 
  W.set_line_width(2);
  
rat_point p;
  forall(p,L) W.draw_filled_node(p.to_point());
  //W.draw_circle(C.to_circle(),red);
  forall(C,LC) W.draw_circle(C.to_circle(),red);
  W.read_mouse();
  W.screenshot("extremal_circle");

  return 0;
}

See also:

Voronoi Diagrams

Data Types for 2-D Geometry

Windows and Panels

Minimum Width and Minimum Area Annuli

Curve Reconstruction

Geometry Algorithms

Geometry

Graphs

GeoWin

Manual Entries

Manual Page of Geometry Algorithms


Algorithmic Solutions Software GmbH