| rat_segment |
s |
introduces a variable s of type rat_segment. s is
initialized to the empty segment.
|
| rat_segment |
s(const rat_point& p, const rat_point& q) |
| |
|
introduces a variable s of type rat_segment. s is
initialized to the segment [p, q].
|
| rat_segment |
s(const rat_point& p, const rat_vector& v) |
| |
|
introduces a variable s of type rat_segment. s is
initialized to the segment [p, p + v].
Precondition
v.dim() = 2.
|
| rat_segment |
s(const rational& x1, const rational& y1, const rational& x2, const rational& y2) |
| |
|
introduces a variable s of type rat_segment. s is
initialized to the segment
[(x1, y1),(x2, y2)].
|
| rat_segment |
s(const integer& x1, const integer& y1, const integer& w1, const integer& x2, const integer& y2, const integer& w2) |
| |
|
introduces a variable s of type rat_segment. s is
initialized to the segment
[(x1, y1, w1),(x2, y2, w2)].
|
| rat_segment |
s(const integer& x1, const integer& y1, const integer& x2, const integer& y2) |
| |
|
introduces a variable s of type rat_segment. s is
initialized to the segment
[(x1, y1),(x2, y2)].
|
| rat_segment |
s(const segment& s1, int prec = rat_point::default_precision) |
| |
|
introduces a variable s of type rat_segment. s is
initialized to the segment obtained by approximating the two
defining points of s1.
|
| segment |
s.to_float() |
returns a floating point approximation of s.
|
| void |
s.normalize() |
simplifies the homogenous representation by calling
source().normalize() and target().normlize().
|
| rat_point |
s.start() |
returns the source point of s.
|
| rat_point |
s.end() |
returns the target point of s.
|
| rat_segment |
s.reversal() |
returns the segment (target(),source()).
|
| rational |
s.xcoord1() |
returns the x-coordinate of the source point of s.
|
| rational |
s.xcoord2() |
returns the x-coordinate of the target point of s.
|
| rational |
s.ycoord1() |
returns the y-coordinate of the source point of s.
|
| rational |
s.ycoord2() |
returns the y-coordinate of the target point of s.
|
| double |
s.xcoord1D() |
returns a double precision approximation of s.xcoord1().
|
| double |
s.xcoord2D() |
returns a double precision approximation of s.xcoord2().
|
| double |
s.ycoord1D() |
returns a double precision approximation of s.ycoord1().
|
| double |
s.ycoord2D() |
returns a double precision approximation of s.ycoord2().
|
| integer |
s.X1() |
returns the first homogeneous coordinate of the source point
of s.
|
| integer |
s.X2() |
returns the first homogeneous coordinate of the target point
of s.
|
| integer |
s.Y1() |
returns the second homogeneous coordinate of the source point
of s.
|
| integer |
s.Y2() |
returns the second homogeneous coordinate of the target point
of s.
|
| integer |
s.W1() |
returns the third homogeneous coordinate of the source point
of s.
|
| integer |
s.W2() |
returns the third homogeneous coordinate of the target point
of s.
|
| double |
s.XD1() |
returns a floating point approximation of s.X1().
|
| double |
s.XD2() |
returns a floating point approximation of s.X2().
|
| double |
s.YD1() |
returns a floating point approximation of s.Y1().
|
| double |
s.YD2() |
returns a floating point approximation of s.Y2().
|
| double |
s.WD1() |
returns a floating point approximation of s.W1().
|
| double |
s.WD2() |
returns a floating point approximation of s.W2().
|
| integer |
s.dx() |
returns the normalized x-difference
X2*W1 - X1*W2
of s.
|
| integer |
s.dy() |
returns the normalized y-difference
Y2*W1 - Y1*W2
of s.
|
| double |
s.dxD() |
returns a floating point approximation of s.dx().
|
| double |
s.dyD() |
returns a floating point approximation of s.dy().
|
| bool |
s.is_trivial() |
returns true if s is trivial.
|
| bool |
s.is_vertical() |
returns true if s is vertical.
Precondition s is non-trivial.
|
| bool |
s.is_horizontal() |
returns true if s is horizontal.
Precondition s is non-trivial.
|
| rational |
s.slope() |
returns the slope of s.
Precondition s is not vertical.
|
| int |
s.cmp_slope(const rat_segment& s1) |
| |
|
compares the slopes of s and s1.
Precondition s and s1 are non-trivial.
|
| int |
s.orientation(const rat_point& p) |
| |
|
computes orientation(a, b, p) (see below), where a 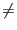 b
and a and b appear in this order on segment s. b
and a and b appear in this order on segment s.
|
| rational |
s.x_proj(rational y) |
returns p.xcoord(), where
p 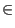 line(s) with
p.ycoord() = y. line(s) with
p.ycoord() = y.
Precondition s is not horizontal.
|
| rational |
s.y_proj(rational x) |
returns p.ycoord(), where
p 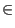 line(s) with
p.xcoord() = x. line(s) with
p.xcoord() = x.
Precondition s is not vertical.
|
| rational |
s.y_abs() |
returns the y-abscissa of line(s), i.e., s.y_proj(0).
Precondition s is not vertical.
|
| bool |
s.contains(const rat_point& p) |
| |
|
decides whether s contains p.
|
| bool |
s.intersection(const rat_segment& t) |
| |
|
decides whether s and t intersect.
|
| bool |
s.intersection(const rat_segment& t, rat_point& p) |
| |
|
decides whether s and t intersect. If so, some point of
intersection is assigned to p.
|
| bool |
s.intersection(const rat_segment& t, rat_segment& inter) |
| |
|
decides whether s and t intersect. If so, the segment formed by the points of intersection is assigned to inter.
|
| bool |
s.intersection_of_lines(const rat_segment& t, rat_point& p) |
| |
|
decides if the lines supporting s and t intersect in a
single point. If so, the point of intersection is assigned to p.
Precondition s and t are nontrivial.
|
| bool |
s.overlaps(const rat_segment& t) |
| |
|
decides whether s and t overlap, i.e. they have a non-trivial intersection.
|
| rat_segment |
s.translate(const rational& dx, const rational& dy) |
| |
|
returns s translated by vector (dx, dy).
|
| rat_segment |
s.translate(const integer& dx, const integer& dy, const integer& dw) |
| |
|
returns s translated by vector
(dx/dw, dy/dw).
|
| rat_segment |
s.translate(const rat_vector& v) |
| |
|
returns s + v, i.e., s translated by vector v.
Precondition v.dim() = 2.
|
| rat_segment |
s + const rat_vector& v |
returns s translated by vector v.
|
| rat_segment |
s - const rat_vector& v |
returns s translated by vector - v.
|
| rat_segment |
s.rotate90(const rat_point& q, int i=1) |
| |
|
returns s rotated about q by an angle of
i x 90
degrees. If i > 0 the rotation is counter-clockwise otherwise
it is clockwise.
|
| rat_segment |
s.rotate90(int i=1) |
returns s rotated about the origin by an angle of
i x 90 degrees.
|
| rat_segment |
s.reflect(const rat_point& p, const rat_point& q) |
| |
|
returns s reflected across the straight line passing
through p and q.
|
| rat_segment |
s.reflect(const rat_point& p) |
| |
|
returns s reflected across point p.
|
| rat_segment |
s.reverse() |
returns s reversed.
|
| rat_segment |
s.perpendicular(const rat_point& p) |
| |
|
returns the segment perpendicular to s with source p
and target on
line(s).
Precondition s is nontrivial.
|
| rational |
s.sqr_length() |
returns the square of the length of s.
|
| rational |
s.sqr_dist(const rat_point& p) |
| |
|
returns the squared Euclidean distance between p and
s.
|
| rational |
s.sqr_dist() |
returns the squared distance between s and the origin.
|
| rat_vector |
s.to_vector() |
returns the vector s.target() - s.source().
|
| bool |
s == const rat_segment& t |
returns true if s and t are equal as oriented segments
|
| int |
equal_as_sets(const rat_segment& s, const rat_segment& t) |
| |
|
returns true if s and t are equal as unoriented segments
|